Differentiable Architecture Search (DARTS)

Introduction

저번 포스팅에서 Neural Architecture Search가 무엇인지 간략하게 설명하였다. 이번에는 내가 석사논문연구를 하면서 사용한 NAS방법론인 Differentiable Architecture Search (Liu et. al 2019)에 대해서 다루어 보겠다. 이 포스팅에서는 DARTS의 수학적 원리를 주로 설명할 것이다.

DARTS 이전의 다른 NAS방법론들은 대부분 이산적인 (discrete) search space를 정의하고 거기서 candidate architecture를 샘플링하고 evaluate 하는 작업을 반복하는 방식으로 탐색을 수행하였다. 이러한 방법들은 보통 탐색한번에 수천개에서 많게는 수만개에 달하는 architecture를 evaluate 해야했기때문에 리소스가 굉장히 많이 소요된다는 단점이 있었다. 이러한 점을 극복하기 위해 DARTS는 이산적인 search space에 continuous relaxation을 하여 미분을 가능케 하였고, gradient descent를 통한 빠르고 효율적인 architecture search를 수행할 수 있게 만들었다. 이 글에서 DARTS가 어떻게 search space를 연속적으로 만들었고, 어떠한 방식으로 search가 이루어지는지 알아보자.

DARTS의 학습과정은 search와 evaluation 두개의 phase로 나누어진다. Search phase에서는 meta-network라고 하는 네트워크가 정의되고 그것의 파라미터들이 학습된다. 그리고 Evaluation phase에서는 학습된 meta-network를 바탕으로 우리가 얻고싶은 최종 네트워크를 derive한 후 그것을 처음부터 다시 학습시킨다. 하나씩 천천히 알아보자.

Search Phase

Architecture Search

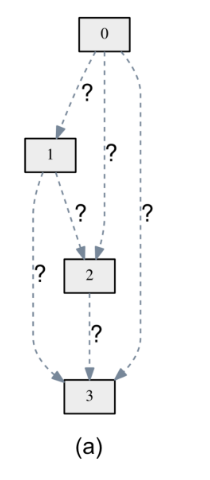
DARTS가 어떤 방식으로 NAS를 수행하는지 설명하기 위헤, 간단한 예를 하나 들겠다. 위 그림의 (a)같이 4개의 노드를 가진 direct acyclic graph (DAG) 형태의 네트워크의 구조가 있고, 아직 어떤 operation을 사용하여 노드들을 연결할지 모른다고 하자. 여기서 노드는 데이터의 latent representation이고 화살표 (connection)들은 convolution, pooling 등의 operation 이다. 그리고 우리는 각 connection마다 3개의 candidate operation, 즉 convolution, pooling, none(연결이 없다는 뜻) 중에서 하나를 골라 부여해주어 네트워크를 만들고 싶다고 하자.

이렇게 DAG의 구조를 가지는 네트워크에서 각 노드의 값은 이렇게 계산이 된다:

\[x^{(j)} = \sum_{i < j} o^{(i, j)}(x^{(i)}) \tag{1}\]

여기서 $x^{(i)}$ , $x^{(j)}$ 는 각각 $i$, $j$ 번째 노드의 값이고 $o^{(i, j)}$ 는 $i$ 번째 노드와 $j$ 번째 노드를 연결하는 operation 이다. 풀어 말하면, $j$번째 노드의 값은 그것의 상위 노드들(parent nodes)의 값에 각각 그 connection에 상응하는 operation을 적용한 값들의 합이다. 예를 들어, 아래 그림과 같이 노드2의 값은 노드0의 값에 $o^{(0, 2)}$를 적용한 것과 노드1의 값에 $o^{(1, 2)}$를 적용한 값의 합이 되겠다.

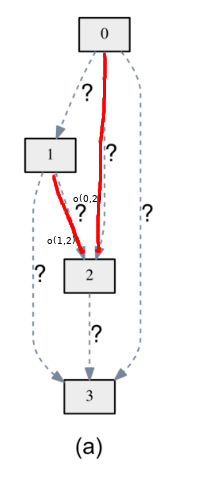
이러한 계산방식은 sequential한 형태의 네트워크가 latent representation의 값을 계산하는 일반적인 형식이다. 그런데 여기서 우리가 해결하고 싶은 것은 각 $o^{(i, j)}$가 어떤 operation이어야 네트워크가 최적이 되느냐이다. 각 $o^{(i, j)}$가 될 수 있는 operation이 3개라면 (convolution, pooling, none) 총 6개의 화살표가 있으니 만들 수 있는 네트워크의 갯수가 총 3^6=729가지가 된다. 당연히도 이모든 경우의 수를 각각 실험 해보기엔 시간이 너무 오래 걸릴것이다.

그래서 DARTS는 어떻게 이 문제를 해결할까? 답은 바로 그림의 (b)같이, 노드를 연결하는 모든 connection들이 하나의 operation이 아닌 3개의 candidate operations 의 가중합 (weighted sum) 이라고 보는 것이다. 논문에선 이 연산자를 mixed operation이라고 부른다 (이렇게 mixed operation을 사용하여 만들어진 네트워크를 meta-network라고 부른다).

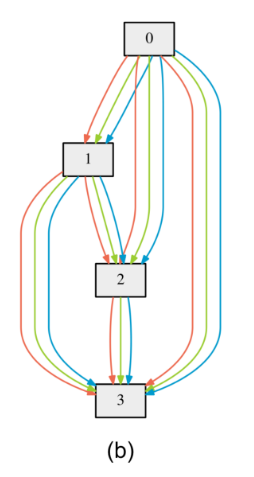
Mixed operation 을 사용하여 latent representation의 값을 구하는 수식을 알아보자. $O$를 모든 operation들의 집합 (e.g., convolution, pooling, none)이라고 하자 (operation $o(\cdot)$는 $x^{(i)}$를 transform 하는 함수라 볼수있다). 그렇다면 mixed operation은 이렇게 표현할 수 있다:

\[\bar{o}^{(i,j)}(x) = \sum_{o \in O} \frac{\exp({\alpha_{o}^{(i,j)}})} {\sum_{o' \in O} \exp(\alpha_{o'}^{(i,j)})} o(x) \tag{2}\]

여기서 $\bar{o}^{(i,j)}$는 노드 $i$ 와 노드 $j$ 사이의 mixed operation 이고 $\alpha^{(i,j)}$는 connection $(i, j)$의 operation들의 가중치들을 가지는 벡터이다 (그러니까 $\alpha_{o}^{(i,j)}$는 connection $(i, j)$안의 operation $o$의 가중치). 수식을 잘 보면, 분수형태는 각 가중치의 softmax를 구하는 것임을 알 수 있다. 그리고 softmax된 각 가중치 를 각 $o(x)$ 에 곱한 후 그 값들을 전부 더하면 mixed operation의 값을 구할 수 있다. 최종적으로, mixed operation을 사용하여 한 노드의 값을 구하려면, $(1)$의 식에 $o^{(i, j)}$ 를 $\bar{o}^{(i, j)}$로 바꿔주면 된다.

operation $o$의 가중치 $\alpha_{o}^{(i,j)}$는 무엇을 의미할까? 바로 connection $(i, j)$에서의 $o$의 strength다. 특정 $\alpha_{o}^{(i,j)}$가 크면 클수록, $\bar{o}^{(i,j)}(x)$의 값이 $o$의 영향을 많이 많이 받고, 반대로 특정 $\alpha_{o}^{(i,j)}$ 가 0에 수렴 할수록 그 $o$는 아무 역할도 하지 않게된다. 극단적인 예로, $\alpha^{(i,j)} = [\alpha_{Conv}^{(i,j)}, \alpha_{Pool}^{(i,j)}, \alpha_{None}^{(i,j)}] = [1, 0, 0]$ 이라고 해보자. 그러면 $\bar{o}^{(i, j)}(x) = Conv(x)$ 가 된다.

이제 우리가 왜 mixed operation을 사용하는지 슬슬 감이 온다. 우리가 정의한 가중치들은 연속적인 변수이고, 그것은 곧 가중치들을 gradient descent를 사용하여 validation loss가 최소가 되도록 학습할 수 있다는 뜻이 된다. DARTS의 메인 아이디어는 바로 이 가중치들을 학습하여 각 connection마다 어떤 operation이 가장 좋은 operation인지를 탐색하는 것이다. 그리하여 우리는 네트워크 구조 최적화문제를 최적의 $\alpha = \{\alpha^{(i,j)}\}$를 찾는 문제로 변환시킬수 있다.

Cell-based Structure

지금까지 DARTS에서 search space가 어떻게 정의 되고 어떻게 미분 가능한 연속적인 형태를 가지게 되었는지 알아보았다. 그런데 여기서 짚고 넘어갈 것이 있다. 위에서 예로 든 그림에서는 노드가 4개 밖에 없었지만 현실에서 NAS를 수행할때 우리는 그보다 훨씬 더 깊은 네트워크의 구조를 탐색하고 싶다. 그런데 우리가 위와 같은 방식으로 모든 노드를 DAG형태로 연결하게 되면, 노드의 갯수가 늘어날수록 connection의 갯수가 기하급수적으로 늘어나게 되고 계산량도 급격히 많아져서 효율적인 NAS를 수행할수 없게 된다. 그래서 DARTS는 네트워크를 여러개의 작은 cell으로 나누고, 그 cell들이 sequential 하게 쌓여있는 형태로 search space를 구성한다.

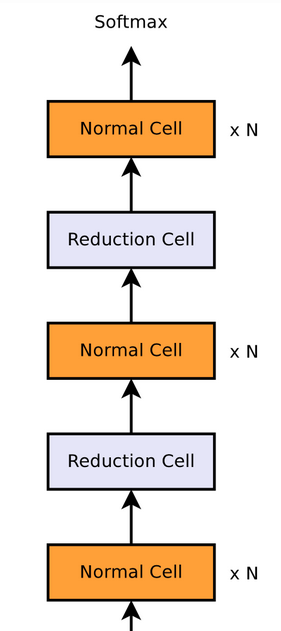
위의 그림에서 하나의 cell이 작은 DAG 형태의 네트워크라고 생각하면 된다. 그림에서 normal cell과 reduction cell 두가지 종류의 cell이 있는데 normal cell은 input의 spatial resolution (여기선 CNN을 예로 든다)을 변화시키지 않는 cell 이고, reduction cell은 input의 resolution 을 절반으로 줄이는 cell이다. 이는 CNN을 만들때 점차적으로 resolution을 줄이고 싶을때 사용할 수 있지만 꼭 그렇게 하지 않아도 되고, CNN이 아닌 다른 종류의 네트워크 구조를 탐색하면 cell이 다른 형식으로 만들어 질 수도 있을 것이다. 이건 구현자 맘이다.

Optimization

다시 돌아와서, DARTS가 어떻게 search space를 연속적으로 만드는지를 알아 보았으니, 이제 정확히 어떻게 $\alpha$가 학습되는지 알아보자.

DARTS의 목표는 validation loss $L_{val}$가 최소가 되게하는 $\alpha$, 즉 $\alpha^{\ast}$ 를 찾는 것이다. 그런데 여기서 주의할 점이 있다. 우리가 학습시킬 meta-network에는 $\alpha$뿐만 아니라 각 operation이 가지는 weights $w$도 있고 (pooling 같이 학습 파라미터가 없는 경우를 제외하면) $\mathcal{L}_{val}$는 이 두변수 모두에게 영향을 받는다는 것이다 (training loss도 마찬가지). 더군다나, $\alpha$와 $w$도 서로의 값에 따라 영향을 받는다. 이러한 constraint가 있을때, DARTS는 어떻게 두 변수를 최적화 할까? 논문의 수식을 살펴보자:

\[\underset{\alpha}{\min} \ \mathcal{L}_{val}(w^{\ast}(\alpha), \alpha) \\ s.t. w^{\ast}(\alpha) = \underset{w}{argmin} \ \mathcal{L}_{train}(w, a) \tag{3}\]

이렇게 두개의 변수가 있고, 그중 하나의 최적와 문제가 ($w$) 다른 하나 ($\alpha$)의 최적화 문제에 nested 되어있는 문제를 bilevel optimization problem 이라고 한다 (GAN의 학습방식과 유사하다는 것을 알 수 있다). DARTS는 이 문제를 $\alpha$를 validation loss로, $w$를 training loss로 번갈아 업데이트하며 최적화 하는 방식으로 해결한다. 그런데 (3)의 식을 보면, $\alpha$를 업데이트할때 $w$가 현재의 $\alpha$가 주어졌을때 $L_{train}$에 대해 최적화 되어있어야 한다는 조건이 있다. 그말은 즉 $\alpha$의 gradient: $\nabla_{\alpha} L_{val} (w^{\ast} (\alpha), \alpha)$를 매 스텝 마다 계산할때마다 $w$를 convergence 까지 학습시켜야 한다는 말이다. 알고리즘이 학습하면서 $\alpha$의 업데이트가 최소 수만번은 업데이트 될 텐데 그때마다 네트워크의 $w$를 새로 학습시키면 당연히 너무 오래 걸릴 것이다. 그래서 논문의 저자들은 $w$를 한 스텝만 gradient update해서 $w^{\ast} (\alpha)$를 근사하자고 제안한다:

\[\nabla_{\alpha} L_{val} (w^{\ast} (\alpha), \alpha) \\ \approx \nabla_{\alpha} L_{val} (w - \xi \nabla_{w} L_{train}(w, \alpha), \alpha) \\ %= \nabla_{\alpha} L_{val} (w^{\prime}, \alpha) - \xi \nabla^{2}_{\alpha, w} L_{train} (w, \alpha) \nabla_{w^{\prime}} L_{val} (w^{\prime}, \alpha), \tag{4}\]

여기서 $w$는 현재의 weight값이고 $\xi$는 $w$를 gradient update할 때의 learning rate이다. 저자들은 이렇게 $w^{\ast} (\alpha)$를 근사해서 bilevel optimization을 했을때 학습변수들의 값이 수렴한다는 증명은 없지만 경험적으로 $\xi$의 값을 올바르게 설정했을때 알고리즘이 수렴했다고 한다.

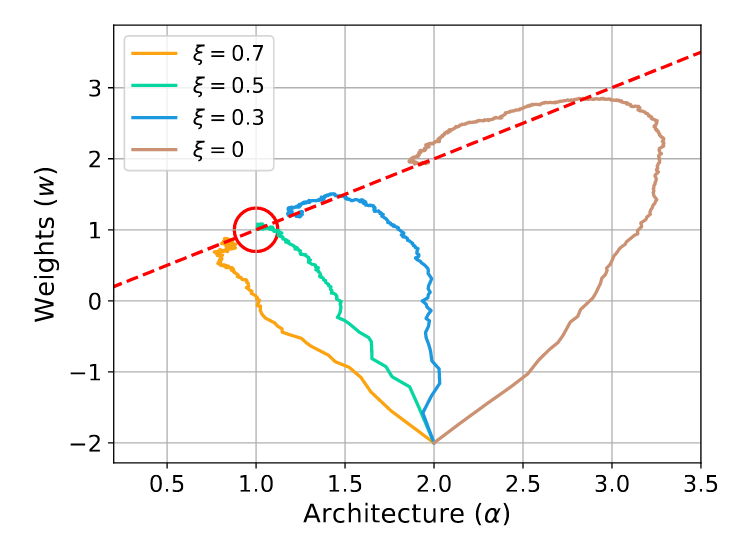
위 그래프는 $\xi$의 값이 변화함에 따라 $\alpha$와 $w$가 어떻게, 어디로 수렴하는지를 보여준다. 빨간 동그라미가 global optimum이고 빨간 점선은 local optimum이다. $\xi$값을 적절히 조정하였을때 알고리즘이 global optimum으로 수렴하는것을 볼 수 있다.

First Order Approximation

근데 그래프를 보면 $\xi$가 0 일때도 어느정도 global optimum으로 수렴하는 것을 볼 수 있다. $\xi = 0$이 무엇을 의미할까? (4)의 식에 대입해보자.

\[\nabla_{\alpha} L_{val} (w^{\ast} (\alpha), \alpha) \\ \approx \nabla_{\alpha} L_{val} (w - 0 \cdot \nabla_{w} L_{train}(w, \alpha), \alpha) \\ = \nabla_{\alpha} L_{val} (w, \alpha) \\ \tag{5}\]

$w^{\ast} (\alpha) = w$ 가 되었다. 이는 곧 “우리는 매 $\alpha$ 업데이트 스텝마다 현재의 $w$ 가 이미 주어진 $\alpha$에 대해 최적이라고 간주하겠어” 라고 하는거다. 다시 말해, $w^{\ast}(\alpha)$를 전혀 approximate 하지 않는 것이다. 이를 논문에서는 first-order approximation 이라고 한다. 그 이유는 (4)의 식에서 chain-rule을 사용하여 gradient를 계산해보면 Hessian 항이 나오는데 ($\nabla_{\alpha}$와 $\nabla_{w}$가 있어서 $\nabla^{2}_{\alpha, w}$가 나온다. 자세한건 논문 참조) $\xi$를 0 으로 설정하면 이 Hessian 항이 사라져서 그렇다. First-order approximation을 사용하면 더 빠르게 계산할 수 있지만 대신 성능이 하락할 수 있는 일종의 cost-performance trade-off로 볼 수 있다.

사실, 우리 연구소에서 여러 실험을 해본결과, Hessian 항을 사용했을때 계산시간은 엄청 늘어나는데 비해 성능은 그다지 높지 않거나 오히려 떨어질때가 많았다. 그래서 나는 개인적으로 DARTS를 써보고 싶은 분들에게 왠만하면 first-order approximation을 쓰라고 권하겠다. 물론 시간과 리소스가 넘친다면 둘 다 해보는게 최선이겠지만.

Architecture Search Summary

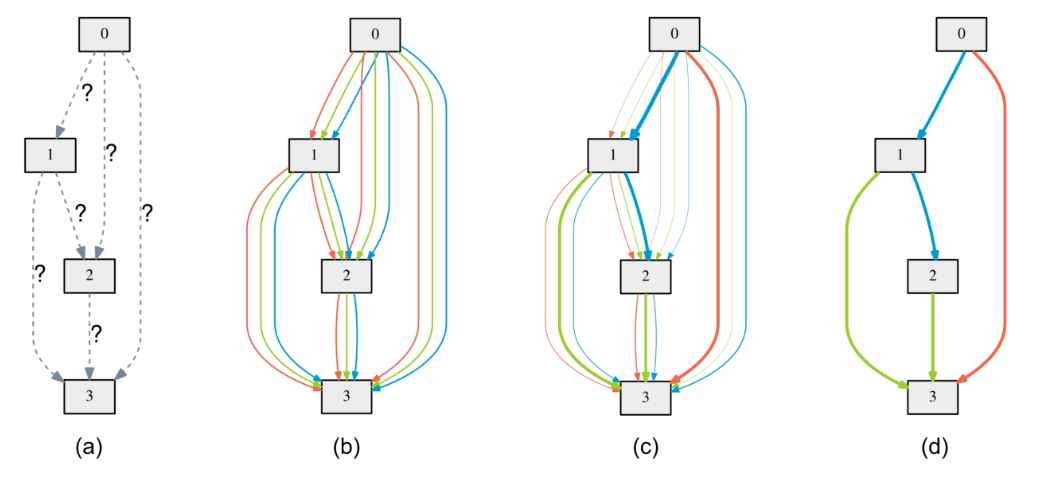
위 pseudocode를 보면 지금까지 설명한 search phase가 어떻게 작동하는지 알 수 있다. 먼저 mixed operations을 정의하여 meta-network를 만들고 $\alpha$와 $w$를 initialize 해준 후 (아래 그림의 b), $\alpha$로 $L_{val}$를, $w$로 $L_{train}$를 한번씩 번갈아가며 업데이트 해준다. 네트워크가 수렴하면 (c) search phase가 끝난다. 이제 이 meta-network로 부터 우리는 discrete network를 derive 한 후 (d) evaluate 해야한다. 어떻게 하는지 알아보자.

Discretization Step

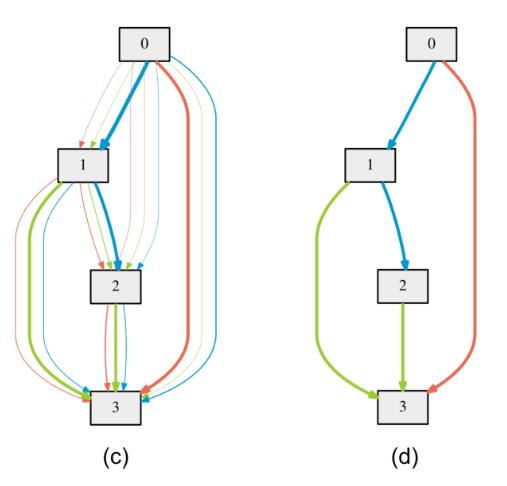
학습이 끝난후, DARTS는 각 노드마다 자신과 그 노드의 모든 상위노드 (previous node) 사이의 operation들을 모아서 그 중 $k=2$개의 가장 큰 strength 를 가진 operation을 남겨두고 나머지는 전부 버려서 discrete한 architecture를 만든다. 여기서 strength는 $\alpha$를 softmax한 값, 즉 $ \frac{\exp({\alpha_{o}^{(i,j)}})} {\sum_{o’ \in O} \exp(\alpha_{o’}^{(i,j)})} o(x)$를 의미한다. $k$는 여기서 하이퍼파라미터로 취급되어 구현자 맘대로 바꿔줄 수 있다. 위의 그림에서도 노드2는 하나의 operation이 남겨진 반면, 노드3은 3개가 남았다. 이렇게 network를 discretize해준 후 얻어진 final network를 처음부터 다시 학습시키면 DARTS를 이용한 NAS가 완성된다.

사실 DARTS의 여러 맹점중 하나가 바로 이 discretization step인데, 그 이유는 search phase에서 학습시킨 meta-network에서 거의 모든 operation들을 버려서 만든 final network가 성능이 좋다는 보장이 없기 때문이다. 이는 meta-network와 final network간의 괴리가 너무 심해서 발생하는데 이 현상을 optimization gap 이라고 부른다. 그래서 이 점을 보완하기위한 후속연구도 진행되었고 (Progressive DARTS), 내 석사논문에서도 이를 보완 하려고 여러 실험을 해보았다. 이 부분은 나중에 후속연구들을 다룰때 더 자세히 설명해 보도록 하겠다.

Experimental Results

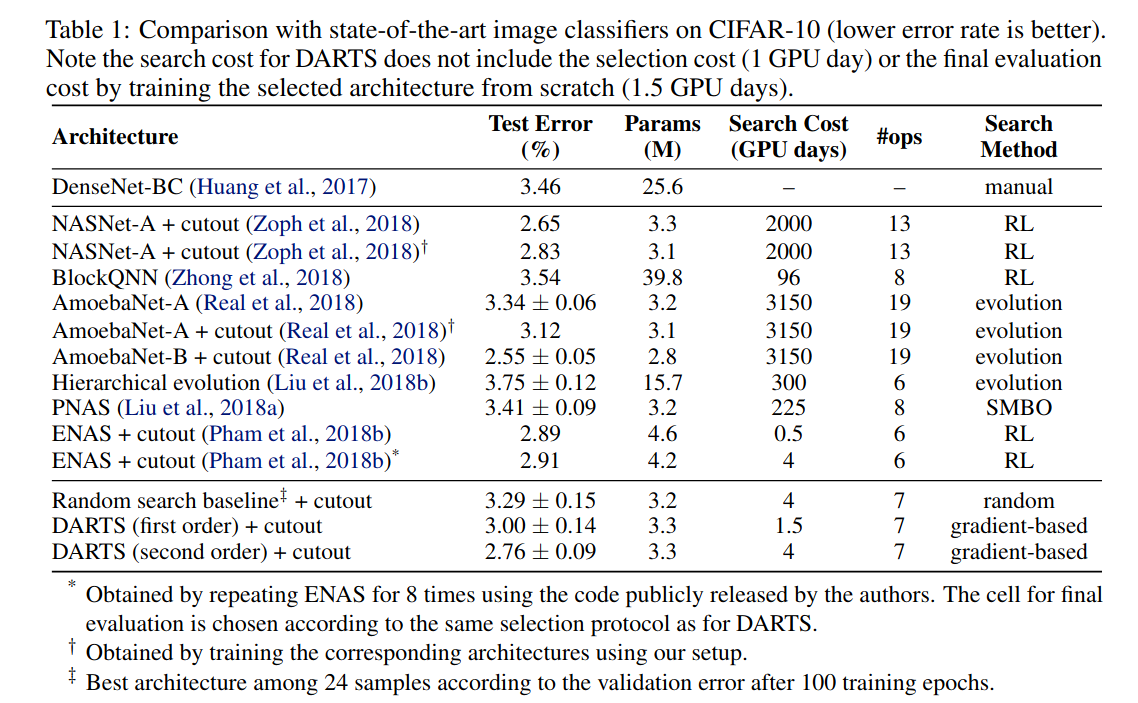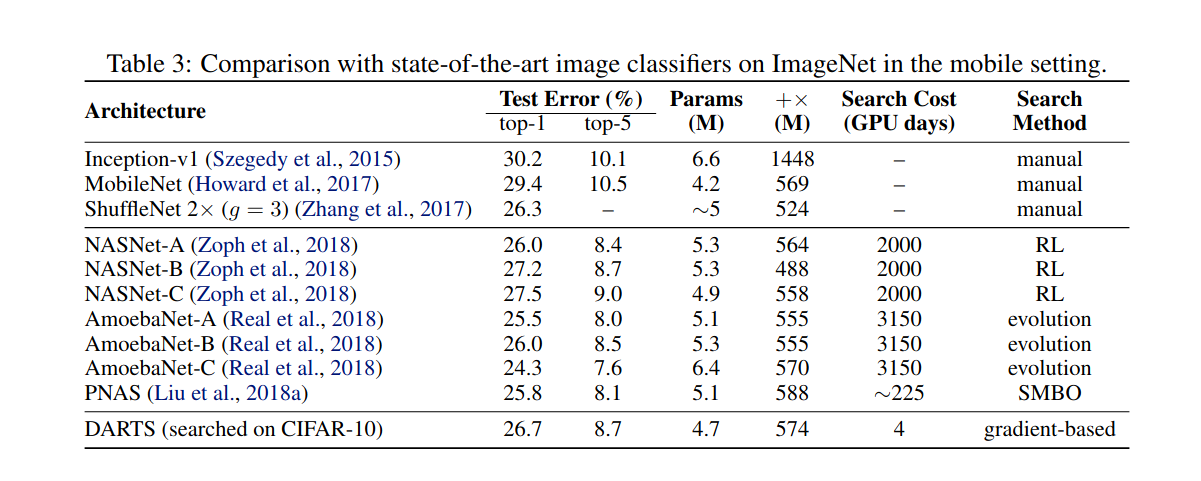위의 표는 DARTS를 통해 image classifier를 CIFAR-10과 데이터들을 학습한 결과를 다른 NAS방법들과 비교한 표이다. second order를 사용하여 얻은 결과가 state-of-the-art는 아니지만 비슷한 성능을 내고, 그에비해 대부분의 강화학습이나 evolution기반의 NAS방법들에 비해 search cost가 현저히 적다는 것을 볼 수 있다. NAS의 특징중 하나는 한 데이터셋으로부터 얻어진 네트워크 구조를 가지고 다른 (보통 더 큰) 데이터셋에 학습시킬 수 있다는 점이다 (이를 transfer learning 이라고 부른다). 위의 표는 CIFAR-10으로 부터 얻어진 구조를 가지고 ImageNet에 학습시켰을때 나온 결과를 비교하였는데, transfer가 상당히 잘 된것을 볼 수 있다.

Conclusion

DARTS는 처음으로 gradient descent를 통한 빠르고 효율적인 NAS의 방법론을 제시했고, 실험결과들이 이 방법론의 실용가능성을 보여주었다. 하지만 현재시점에서, 사실 DARTS가 잘 작동하지 않는다는 논문들도 많이 발표되었고, 이를 보완하기위해 많은 후속연구가 이루어지고 있다. 이 포스팅은 NAS와 DARTS에 관심이 있으신 분들에게 DARTS의 수학적 작동원리를 설명드리기 위해 작성하였다. 다음 포스팅에서는 DARTS의 단점을 살펴보고, 후속연구들이 이를 어떤 다양한 방식으로 보완하려 했는지 알아보겠다. DARTS의 코드는 저자들이 공개해 놓았으니 관심이 있는 분들은 한번 살펴보고 사용해보길 권하겠다. 그리고 이 포스트는 DARTS논문의 내용중 길이 관계상 다루지 않은 것들(cell간 weight sharing, cell안의 input connection의 갯수와 cell간 connection 등)도 있으니 논문을 직접 확인해 보는 걸 추천드린다.